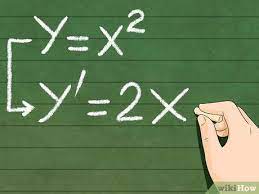The world is shaped by mathematical intricacies, with calculus being a fundamental branch that unlocks the secrets of change and motion (Simplilearn, 2023). This blog is designed for beginners, offering a captivating journey through the basics of calculus. Whether you’re an aspiring mathematician, engineering enthusiast, or curious about the forces shaping our universe, this guide will make calculus accessible, engaging, and enjoyable. So, buckle up and get ready to delve into the realm of derivatives, integrals, and limits. As we navigate this landscape together, you’ll discover the beauty and elegance that calculus brings to the world, and you’ll gain the confidence to tackle mathematical challenges with newfound enthusiasm. Let’s embark on this journey of Calculus for beginners’ discovery and unravel the mysteries of calculus—one concept at a time.
What is Calculus?
Calculus is a branch of mathematics that focuses on change, providing tools to understand how things shift, evolve, and transform. It helps predict, analyze, and manipulate various phenomena. It encompasses two key concepts: differentiation and integration. Differentiation is a magnifying glass for change, allowing us to analyze how a quantity changes as another quantity changes. Integration, on the other hand, is like a puzzle solver, helping us piece together smaller bits of information to understand the bigger picture.
Calculus is crucial in understanding change and rates, as it allows us to calculate the slope of a curve at any point and find the total change within a region. It transcends its mathematical realm and underpins countless scientific, engineering, and economic discoveries, from predicting projectile trajectories to optimizing investment strategies. It is the bedrock of innovation and problem-solving.
Fundamental Concepts
The fundamental concepts of calculus are functions, limits, continuity, and derivatives. Functions are the magical machines that transform input into output, with various representations such as graphs, equations, and tables. Limits in calculus capture the idea of approaching a value as something else changes, while continuity ensures smooth paths without unexpected potholes. Derivatives, the superhero of calculus, measure the rate of change in a function as its input changes. They reveal hidden patterns and behaviors in the world around us, such as the speed of an object in motion or the cost function of a business. By grasping these fundamental concepts, we can explore the intricacies of calculus and gain a deeper understanding of change itself.
Do my online class for me services are now available for students to avail online.
Differentiation: The Basics
Differentiation is a powerful tool that helps us understand the essence of change in the world around us (BAW, 2022). It involves focusing on the intricate details of curves, lines, and functions, allowing us to unravel the dynamics of motion, growth, and transformation. Derivatives measure how a function changes as its input changes, providing insights into its behavior. Calculating derivatives using basic rules, such as the power rule, product rule, quotient rule, and chain rule, is essential for understanding complex functions. Derivatives have profound real-world implications, such as analyzing roller coasters, optimizing production, pricing, and profit, and understanding the velocity and acceleration of objects in motion.
They also play a crucial role in medicine, biology, finance, and other fields, modeling and predicting phenomena. As we immerse ourselves in differentiation, we unlock a new way of seeing and understanding the universe, unlocking the essence of change and the heartbeat of life itself.
Rules of Differentiation
Differentiation rules are essential tools in Basic calculus principles that help us understand complex functions and their transformations. These rules include the Power Rule, Product Rule, and Quotient Rule. Power rules differentiate functions raised to power, while product rules differentiate products and fractions. The quotient rule guides in differentiating fractions, while the chain rule helps dissect composite functions, revealing how changes in one layer affect the whole. Applying these rules to real examples helps understand the rate of population growth, rocket launch velocity, and the overall motion of a system.
These rules are the foundation of calculus, and as we practice, we become masters of differentiation through application. By embracing these rules as our artistic tools, we can gain intricate insights into the world of functions, changes, and the beauty of mathematics.
Applications of Differentiation
Differentiation is a powerful tool for understanding real-world scenarios, such as finding slopes and rates of change, optimizing problems, and solving related rates problems. It helps us understand the dynamic interplay between variables in complex situations, such as the trajectory of a projectile or the growth of a bacterial population. Differentiation allows us to visualize the intricate workings of the world and decode nature’s language of change, revealing the elegance of mathematics in action. By mastering differentiation, we gain the ability to decode nature’s language of change and glimpse the elegance of mathematics in action.
Integration: The Basics
Integration, the second major pillar of calculus, is the process of finding the area under a curve and accumulating quantities over time. It unlocks mathematical insights by reversing differentiation and seeking the antiderivative of a function. Integration comes with basic rules like the power rule, constant multiple rules, and sum rule, which unlock new mathematical landscapes. Geometric interpretation of integration involves visualizing a function graphed on a coordinate plane, revealing the area between the curve and the x-axis within that interval. Integrating allows us to explore the entirety of change, uncovering hidden insights and transforming our perception and understanding of the world around us. If you find this hard you can always hire, take my calculus exam for me online service.
Techniques of Integration
Integration is a complex and multifaceted process, with advanced techniques like substitution, integration by parts, and partial fraction decomposition helping mathematicians navigate complex expressions. The substitution method exposes hidden patterns, while integration by parts breaks down complex integrals into manageable parts. Partial fraction decomposition untangles complex fractions by breaking them down into simpler components, providing a systematic approach to solving intricate equations. Mastering these techniques helps decipher mathematical intricacies and reveal elegant solutions. By embracing the artistry of mathematical exploration, mathematicians can expand their calculus toolkit and tackle even the most enigmatic integrals.
Applications of Integration
Integration is a powerful tool in mathematics that unlocks profound insights into the physical and mathematical universe. It helps us measure enclosed spaces, find the volume of solids of revolution, and calculate work and displacement. Integration is not limited to mathematics but also forms the backbone of physics, translating abstract concepts into tangible quantities. By integrating, we can understand and predict real-world phenomena, transforming abstract concepts into tangible quantities. By embracing the practical power of integration, we can decipher the language of the universe and gain a deeper understanding of the world.
Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a crucial cornerstone in the field of calculus, bridging differentiation and integration. It reveals the deep interplay between these two powerful tools, illuminating the relationship between functions and their accumulations. The theorem consists of two parts: the First Fundamental Theorem, which asserts that the definite integral of a function can be evaluated by finding its antiderivative and evaluating it at the endpoints of the interval, and the Second Fundamental Theorem, which states that the derivative of a function is the original function itself.
This harmony between differentiation and integration highlights the reciprocal nature of these operations and their symbiotic relationship. The Fundamental Theorem unlocks the essence of calculus, revealing the intricate connections between functions, their derivatives, and accumulated values, making calculus a unified language for seamless navigation between the microcosmic world of instantaneous change and the macrocosmic realm of accumulation.
References
BAW (2022). How Academic Help Providers Save the Students’ Future? https://bestassignmentwriter.co.uk/blog/how-academic-help-providers-save-the-students-future/
Simplilearn (2023). Data Analytics Tutorial for Beginners: A Step-By-Step Guide. https://www.simplilearn.com/tutorials/data-analytics-tutorial