[ad_1]
Far more than a century ago, Srinivasa Ramanujan shocked the mathematical planet with his extraordinary means to see extraordinary designs in figures that no one particular else could see. The self-taught mathematician from India described his insights as deeply intuitive and non secular, and designs typically came to him in vivid desires. These observations captured the remarkable beauty and sheer chance of the abstract earth of pure mathematics. In modern decades, we have begun to see AI make breakthroughs in places involving deep human intuition, and far more recently on some of the hardest challenges throughout the sciences, nonetheless till now, the most current AI approaches have not assisted in important effects in pure maths exploration.
As aspect of DeepMind’s mission to resolve intelligence, we explored the opportunity of machine learning (ML) to realize mathematical constructions and styles, and assist guidebook mathematicians towards discoveries they may possibly in any other case hardly ever have observed — demonstrating for the initially time that AI can help at the forefront of pure mathematics.
Our exploration paper, posted right now in the journal Character, information our collaboration with best mathematicians to utilize AI toward identifying new insights in two places of pure arithmetic: topology and illustration principle. With Professor Geordie Williamson at the University of Sydney, we uncovered a new system for a conjecture about permutations that has remained unsolved for decades. With Professor Marc Lackenby and Professor András Juhász at the College of Oxford, we have learned an surprising relationship concerning different locations of mathematics by studying the composition of knots. These are the very first major mathematical discoveries produced with equipment studying, in accordance to the leading mathematicians who reviewed the perform. We’re also releasing entire companion papers on arXiv for every final result that will be submitted to suitable mathematical journals (permutations paper knots paper). Via these illustrations, we suggest a design for how these resources could be utilized by other mathematicians to obtain new outcomes.

The two fundamental objects we investigated were knots and permutations.
For numerous many years, computers have been utilised by mathematicians to deliver information to enable in the lookup for patterns. Known as experimental mathematics, this sort of exploration has resulted in effectively-recognized conjectures, this sort of as the Birch and Swinnerton-Dyer conjecture — a person of six Millennium Prize Difficulties, the most perfectly-regarded open issues in arithmetic (with a US$1 million prize connected to every). While this tactic has been profitable and is pretty widespread, the identification and discovery of patterns from this details has still relied mostly on mathematicians.
Acquiring patterns has turn out to be even much more crucial in pure maths due to the fact it is now feasible to crank out extra knowledge than any mathematician can reasonably expect to examine in a lifetime. Some objects of desire — this kind of as those with hundreds of dimensions — can also merely be too unfathomable to rationale about immediately. With these constraints in brain, we believed that AI would be capable of augmenting mathematicians’ insights in totally new ways.
It feels like Galileo finding up a telescope and staying ready to gaze deep into the universe of knowledge and see points hardly ever detected ahead of.
Marcus Du Sautoy, Simonyi Professor for the Public Understanding of Science and Professor of Mathematics, University of Oxford
Our results counsel that ML can complement maths research to tutorial intuition about a dilemma by detecting the existence of hypothesised styles with supervised discovering and offering perception into these styles with attribution methods from device discovering:
With Professor Williamson, we utilized AI to aid find out a new technique to a extended-standing conjecture in representation idea. Defying development for practically 40 years, the combinatorial invariance conjecturestates that a romantic relationship should really exist among particular directed graphs and polynomials. Utilizing ML techniques, we had been ready to acquire assurance that this sort of a relationship does indeed exist and to discover that it may be relevant to structures regarded as broken dihedral intervals and extremal reflections. With this knowledge, Professor Williamson was able to conjecture a surprising and attractive algorithm that would address the combinatorial invariance conjecture. We have computationally verified the new algorithm throughout additional than 3 million examples.
With Professor Lackenby and Professor Juhász, we explored knots – a single of the elementary objects of research in topology. Knots not only convey to us about the numerous methods a rope can be tangled but also have shocking connections with quantum subject idea and non-Euclidean geometry. Algebra, geometry, and quantum principle all share exclusive views on these objects and a extensive standing mystery is how these different branches relate: for example, what does the geometry of the knot convey to us about the algebra? We educated an ML design to uncover these a pattern and amazingly, this revealed that a distinct algebraic quantity — the signature — was instantly related to the geometry of the knot, which was not earlier acknowledged or suggested by existing concept. By making use of attribution methods from machine studying, we guided Professor Lackenby to find a new quantity, which we phone the organic slope, that hints at an significant aspect of composition ignored right up until now. With each other we have been then able to prove the specific character of the partnership, creating some of the first connections among these diverse branches of arithmetic.
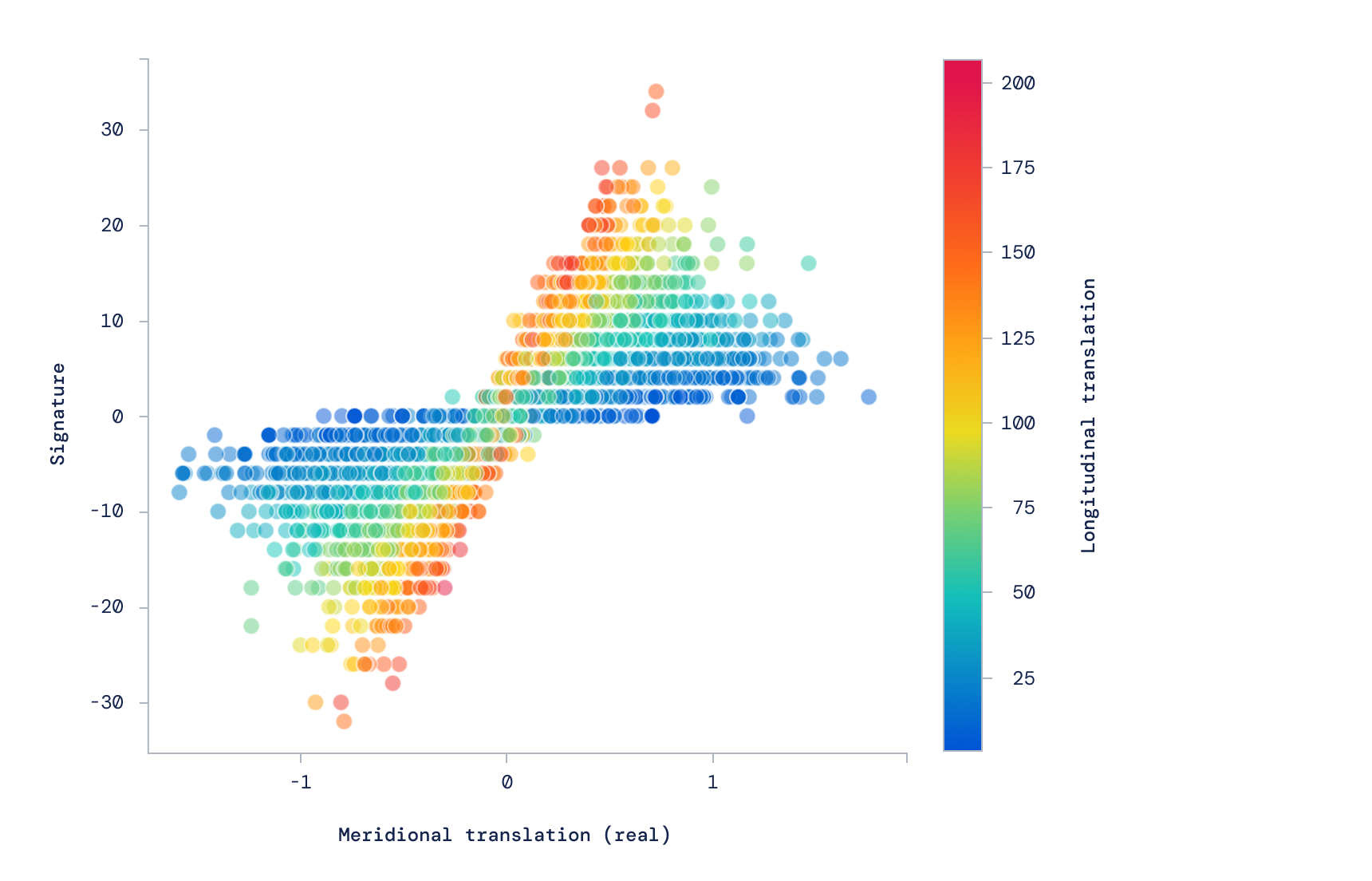
The use of understanding methods and AI systems retains great guarantee for the identification and discovery of patterns in arithmetic. Even if specific kinds of patterns keep on to elude present day ML, we hope our Nature paper can inspire other scientists to take into consideration the opportunity for AI as a beneficial tool in pure maths. To replicate the benefits, any person can obtain our interactive notebooks. Reflecting on the unbelievable thoughts of Ramanujan, George Frederick James Temple wrote, “The great advancements in arithmetic have not been produced by logic but by creative imagination.” Doing the job with mathematicians, we search forward to observing how AI can further elevate the natural beauty of human intuition to new concentrations of creative imagination.
[ad_2]
Supply url


