[ad_1]
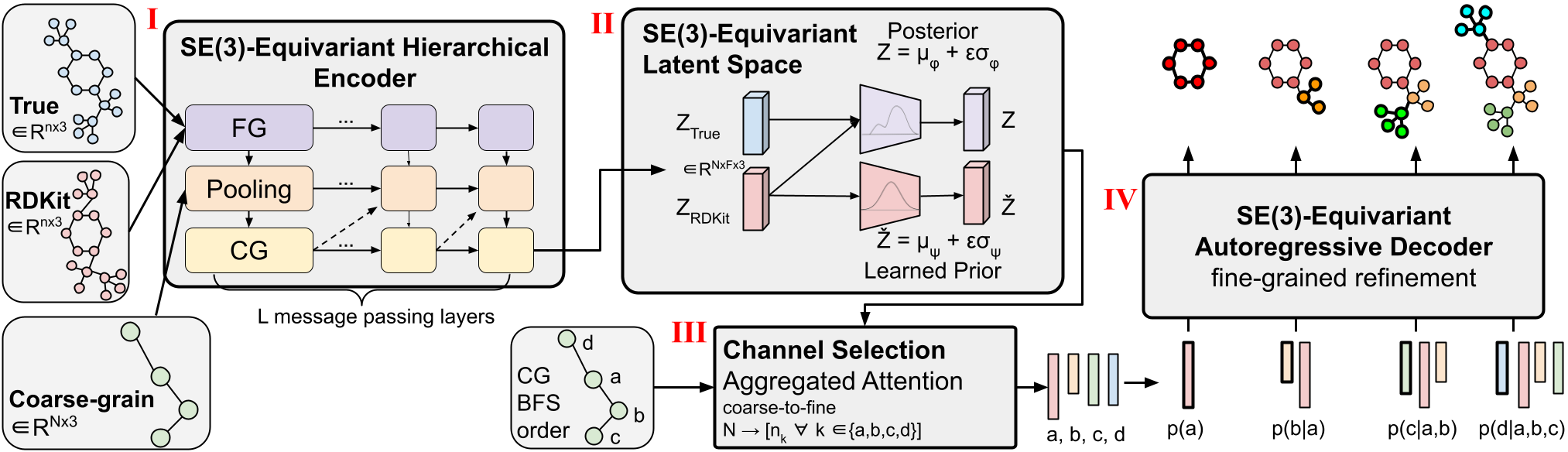
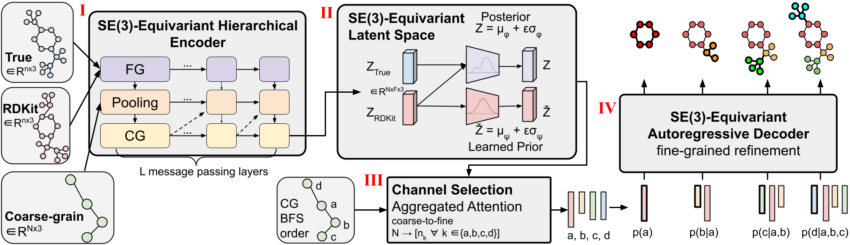
Figure 1: CoarsenConf architecture.
Molecular conformer technology is a elementary job in computational chemistry. The goal is to predict steady reduced-electricity 3D molecular buildings, recognised as conformers, offered the 2D molecule. Exact molecular conformations are crucial for numerous applications that depend on specific spatial and geometric characteristics, which includes drug discovery and protein docking.
We introduce CoarsenConf, an SE(3)-equivariant hierarchical variational autoencoder (VAE) that swimming pools information from high-quality-grain atomic coordinates to a coarse-grain subgraph amount illustration for productive autoregressive conformer generation.
Track record
Coarse-graining lowers the dimensionality of the trouble letting conditional autoregressive technology instead than creating all coordinates independently, as accomplished in prior function. By immediately conditioning on the 3D coordinates of prior produced subgraphs, our model greater generalizes throughout chemically and spatially related subgraphs. This mimics the underlying molecular synthesis system, wherever little practical models bond with each other to sort huge drug-like molecules. In contrast to prior procedures, CoarsenConf generates reduced-electrical power conformers with the ability to design atomic coordinates, distances, and torsion angles immediately.
The CoarsenConf architecture can be broken into the next elements:
(I) The encoder $q_phi(z| X, mathcalR)$ usually takes the great-grained (FG) floor reality conformer $X$, RDKit approximate conformer $mathcalR$ , and coarse-grained (CG) conformer $mathcalC$ as inputs (derived from $X$ and a predefined CG strategy), and outputs a variable-size equivariant CG illustration through equivariant message passing and stage convolutions.
(II) Equivariant MLPs are utilized to discover the mean and log variance of both equally the posterior and prior distributions.
(III) The posterior (training) or prior (inference) is sampled and fed into the Channel Collection module, wherever an awareness layer is applied to understand the exceptional pathway from CG to FG structure.
(IV) Offered the FG latent vector and the RDKit approximation, the decoder $p_theta(X |mathcalR, z)$ learns to get better the minimal-vitality FG construction via autoregressive equivariant concept passing. The entire product can be experienced conclusion-to-end by optimizing the KL divergence of latent distributions and reconstruction mistake of generated conformers.
MCG Process Formalism
We formalize the task of Molecular Conformer Generation (MCG) as modeling the conditional distribution $p(X|mathcalR)$, wherever $mathcalR$ is the RDKit generated approximate conformer and $X$ is the optimal reduced-vitality conformer(s). RDKit, a commonly applied Cheminformatics library, makes use of a inexpensive distance geometry-based mostly algorithm, adopted by an cheap physics-dependent optimization, to achieve reasonable conformer approximations.
Coarse-graining
Determine 2: Coarse-graining Course of action.
(I) Example of variable-duration coarse-graining. Fine-grain molecules are break up alongside rotatable bonds that outline torsion angles. They are then coarse-grained to cut down the dimensionality and master a subgraph-level latent distribution. (II) Visualization of a 3D conformer. Unique atom pairs are highlighted for decoder message-passing functions.
Molecular coarse-graining simplifies a molecule representation by grouping the high-quality-grained (FG) atoms in the authentic composition into person coarse-grained (CG) beads $mathcalB$ with a rule-based mostly mapping, as proven in Determine 2(I). Coarse-graining has been widely used in protein and molecular design and style, and analogously fragment-amount or subgraph-level technology has established to be remarkably important in numerous 2D molecule design duties. Breaking down generative complications into smaller parts is an approach that can be utilized to a number of 3D molecule tasks and delivers a pure dimensionality reduction to permit performing with massive elaborate programs.
We note that as opposed to prior works that emphasis on set-length CG methods where each individual molecule is represented with a preset resolution of $N$ CG beads, our approach works by using variable-size CG for its overall flexibility and means to assist any decision of coarse-graining system. This indicates that a solitary CoarsenConf design can generalize to any coarse-grained resolution as enter molecules can map to any number of CG beads. In our circumstance, the atoms consisting of each and every related part ensuing from severing all rotatable bonds are coarsened into a one bead. This preference in CG technique implicitly forces the design to find out more than torsion angles, as effectively as atomic coordinates and inter-atomic distances. In our experiments, we use GEOM-QM9 and GEOM-Medicines, which on regular, possess 11 atoms and 3 CG beads, and 44 atoms and 9 CG beads, respectively.
SE(3)-Equivariance
A key part when performing with 3D structures is retaining acceptable equivariance.
A few-dimensional molecules are equivariant beneath rotations and translations, or SE(3)-equivariance. We implement SE(3)-equivariance in the encoder, decoder, and the latent house of our probabilistic product CoarsenConf. As a end result, $p(X | mathcalR)$ stays unchanged for any rototranslation of the approximate conformer $mathcalR$. Furthermore, if $mathcalR$ is rotated clockwise by 90°, we count on the optimal $X$ to show the identical rotation. For an in-depth definition and dialogue on the strategies of preserving equivariance, you should see the comprehensive paper.
Aggregated Awareness
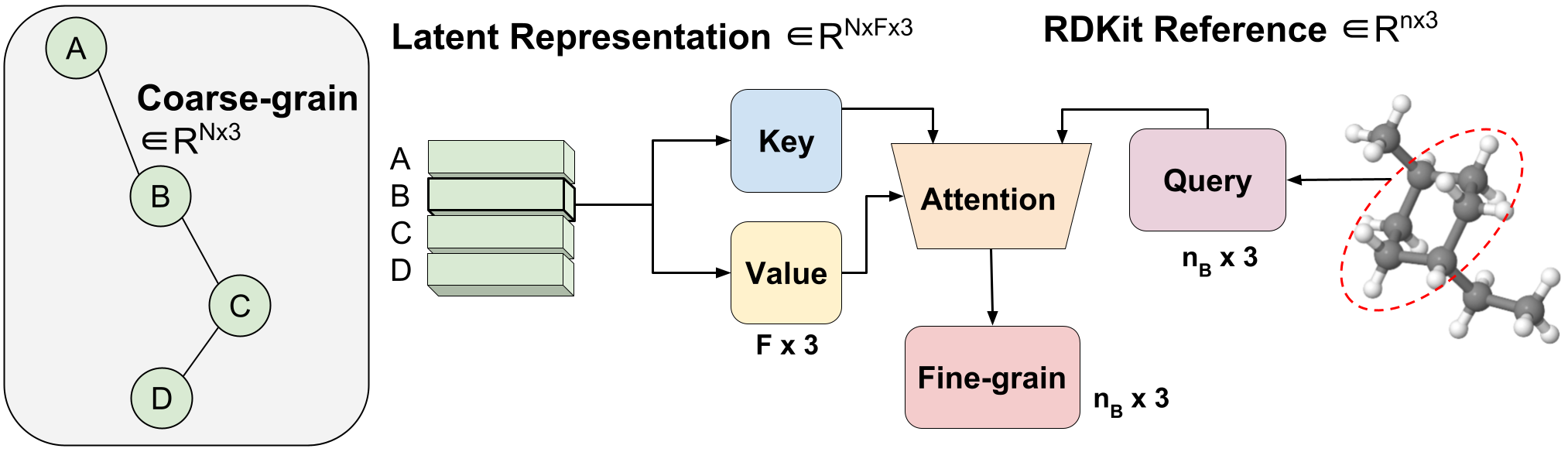
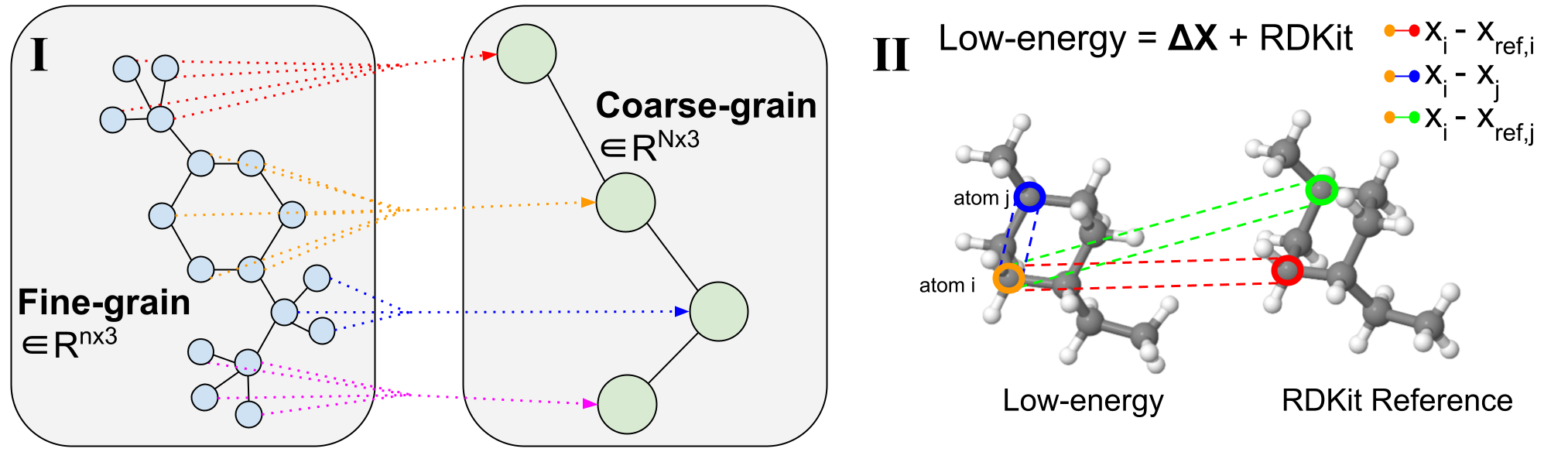
Figure 3: Variable-duration coarse-to-fine backmapping by means of Aggregated Notice.
We introduce a method, which we get in touch with Aggregated Consideration, to understand the optimum variable length mapping from the latent CG representation to FG coordinates. This is a variable-length operation as a single molecule with $n$ atoms can map to any selection of $N$ CG beads (every bead is represented by a single latent vector). The latent vector of a single CG bead $Z_B$ $in R^F instances 3$ is applied as the critical and benefit of a one head awareness procedure with an embedding dimension of three to match the x, y, z coordinates. The question vector is the subset of the RDKit conformer corresponding to bead $B$ $in R^ n_B periods 3$, exactly where $n_B$ is variable-size as we know a priori how numerous FG atoms correspond to a sure CG bead. Leveraging awareness, we efficiently understand the optimum mixing of latent attributes for FG reconstruction. We simply call this Aggregated Notice since it aggregates 3D segments of FG information and facts to kind our latent question. Aggregated Awareness is accountable for the economical translation from the latent CG representation to practical FG coordinates (Figure 1(III)).
Design
CoarsenConf is a hierarchical VAE with an SE(3)-equivariant encoder and decoder. The encoder operates around SE(3)-invariant atom features $h in R^ n instances D$, and SE(3)-equivariant atomistic coordinates $x in R^n moments 3$. A one encoder layer is composed of 3 modules: fine-grained, pooling, and coarse-grained. Entire equations for each individual module can be observed in the whole paper. The encoder makes a final equivariant CG tensor $Z in R^N instances F moments 3$, in which $N$ is the selection of beads, and F is the consumer-outlined latent sizing.
The purpose of the decoder is two-fold. The 1st is to change the latent coarsened representation back again into FG space via a process we call channel assortment, which leverages Aggregated Consideration. The 2nd is to refine the great-grained representation autoregressively to crank out the last reduced-electricity coordinates (Figure 1 (IV)).
We emphasize that by coarse-graining by torsion angle connectivity, our product learns the ideal torsion angles in an unsupervised fashion as the conditional enter to the decoder is not aligned. CoarsenConf ensures each up coming produced subgraph is rotated thoroughly to achieve a low coordinate and distance error.
Experimental Benefits
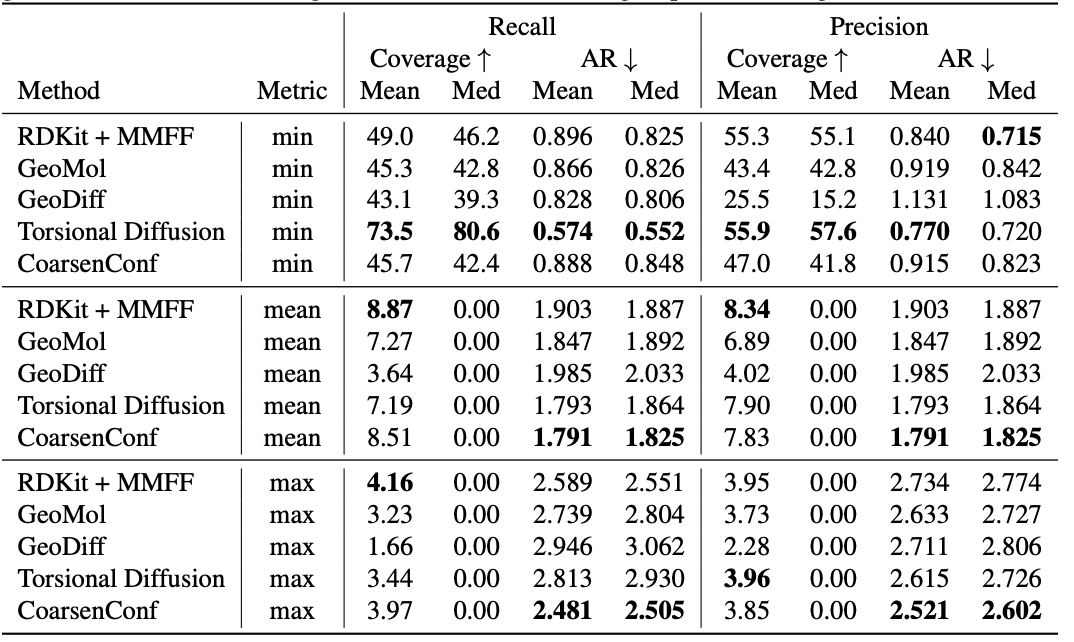
Desk 1: Excellent of created conformer ensembles for the GEOM-Medicines test set ($delta=.75Å$) in phrases of Coverage (%) and Average RMSD ($Å$). CoarsenConf (5 epochs) was restricted to working with 7.3% of the info applied by Torsional Diffusion (250 epochs) to exemplify a minimal-compute and facts-constrained routine.
The typical mistake (AR) is the important metric that steps the normal RMSD for the generated molecules of the proper test established. Coverage actions the proportion of molecules that can be produced inside a distinct mistake threshold ($delta$). We introduce the imply and max metrics to far better evaluate robust era and stay away from the sampling bias of the min metric. We emphasize that the min metric produces intangible outcomes, as except the optimum conformer is identified a priori, there is no way to know which of the 2L produced conformers for a single molecule is ideal. Desk 1 reveals that CoarsenConf generates the lowest average and worst-situation error throughout the full examination established of Medicine molecules. We additional clearly show that RDKit, with an affordable physics-based mostly optimization (MMFF), achieves far better protection than most deep learning-centered approaches. For official definitions of the metrics and additional conversations, please see the total paper connected underneath.
For extra facts about CoarsenConf, read the paper on arXiv.
BibTex
If CoarsenConf evokes your get the job done, you should contemplate citing it with:
@postingreidenbach2023coarsenconf,
title=CoarsenConf: Equivariant Coarsening with Aggregated Consideration for Molecular Conformer Era,
author=Danny Reidenbach and Aditi S. Krishnapriyan,
journal=arXiv preprint arXiv:2306.14852,
yr=2023,
[ad_2]
Source backlink